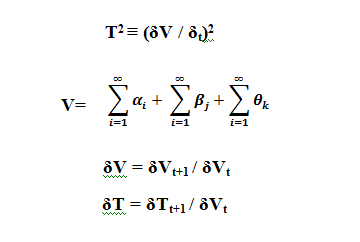Çdo levizje politike ose ekonomike globale apo lokale ka si motiv tre variabla makroekonomikë; prodhimin bruto të mbrëndshëm, papunësinë dhe inflacionin.
Bojaj, gjatë mbrojtjes së magjistruturës, propozon zbatimin e teorisë së relativitetit të Albert Einstein, konceptin E = MC², në mënyrë që të vijmë deri te një model i ri efikas i llogaritjes së PBB-së (Prodhimit Bruto të Mbrënshëm, GDP). Ndërtimi i PBB-së, sipas këtij modeli, kërkon përdorimin e dy variablave ekonomikë në teorinë speciale të relativitetit: normën e rritjes së informacionit (G2B dhe G2C) dhe shpejtësinë e zhvillimit teknologjik.
Bitët dhe çipat kanë ndryshuar anatominë e produkteve dhe ne duhet të analizojmë impaktin e këtyre bitëve në teoritë ekonomike të cilat jane fituesve të Çmimive Nobel. Le të shohim!
Produktet e mëparshme janë krijuar në bazë të punës, teknologjisë dhe kapitalit. Në mënyrë që të prodhohet një kompjuter nevojiten punëtorë. Më shumë kompjutera – më shumë punëtorë. Robert Solow, fitues i çmimit Nobel, ka dalë me një formulë për llogaritjen e ndikimit të progresit teknologjik në produkt. Formula duket si më poshtë:
Mbetja = gy – (αgN + (1-α)gK)
Por kjo formulë na jep efektin e përgjithshëm të teknologjisë në produkt, por ne nuk mund të shohim konkretisht cila teknologji ndikon më së shumti në një produkt dhe deri në çfarë mase. Dhe, më e rëndësishmja, kjo formulë nuk përmban fenomenin e “e-shërbimeve” aktuale.
Pra, ne do të dëshironim të masim ndikimin e e-shërbime ( 20 shërbimeve elektronike të standardizuara nga Komisioni Europian), G2B dhe G2C, në standardin e jetesës. Në fakt, ne do të donim për të parë rregullin “80/20” dhe masën prej të cilave 20%, e G2B dhe G2C,e e-shërbimeve, ofron 80% të produkteve (output) dhe sa energji ekonomike sjell secila nga 20 shërbimet e Komisionit Europian.
Koncepti E=MC²
Megjithatë, ne do të fillojë nga zbatimi i teorisë speciale të relativitetit të Albert Ajnshtajn në makroekonomi. Konstruktimi i produktit Y, në këtë model kërkon përdorimin e dy variablave ekonomike në teorinë speciale të relativitetit: normën e rritjes së informimit dhe shpejtësinë të zhvillimit teknologjik.
Teorija e Ajnshtajnit është e bazuar në bashkimin e dy ligjeve themelore të fizikës në një ligj. Ky ligj quhet teoria speciale e relativitetit. Ligji i ruajtjes së energjisë (C²) dhe ligji i ruajtjes së masës (M) janë shkrirë në një ekuacion të vetëm E = MC².
Sipas teorisë speciale të Ajnshtajnit, ai ka thënë: “Le të fillojmë me faktin se nga teoria speciale e relativitetit masa (M) dhe energjia (E) janë të njëjtat gjëra por manifestime të ndryshme”. Për më tepër, ekuacioni i energjisë (E) është i barabartë me MC², dmth. energjiia është e barabartë me masën (M) shumëzuar me shpejtësinë e dritës në katror, tregon se një sasi shumë e vogël e masës mund të konvertohet në një sasi shumë të mëdhe të energjisë dhe anasjelltas. Masa (M) dhe energjia (E) janë ekuivalente në fakt sipas formulës të cilat janë provuar eksperimentalisht nga Cockcroft dhe Walton në 1932. ” (Ajnshtajn, 1952). Me këtë qasje, le të përdorim teorinë speciale të relativitetit, me qëllim që të matet produkti (output) i 20 shërbimeve elektronike të EU, G2B dhe G2C, për të treguar se është e mundur për të aplikuar formulën E = MC² në analizën makroekonomike. Për të matur Y, le përdorim dy variabla: normën e rritjes së informacionit (I) dhe shpejtësinë e zhvillimit teknologjik (T²).
 Propozmi i konceptit të ri të strukturës së PBB (GDP)
Propozmi i konceptit të ri të strukturës së PBB (GDP)
Së pari, sugjerojmë aplikimin e ekuacionit E = MC² për matjen e shërbimeve specifike që janë treguar më sipër. Prandaj, sugjerojmë që variablat origjinale nga formula E = MC² të zëvendësohen me dy variabla ekonomikë me qëllimë për të matur energjinë makroekonomike Y. Energjinë do ta zëvendësojmë me produktin (output) Y; masën (M) ta zëvendësojmë me normën e rritjes së informacionit “I” dhe C² do ta zëvendësojmë me shpejtësinë e zhvillimit teknologjik “T²”. Së pari, ne propozojmë për të llogaritur normën fillestare dhe përfundimtare të rritjes së informacionit midis dy viteve. Në rastin tonë, do të përdorim derivatin e pjesshëm në bazë të kohës. Ne kemi dy periudha kohore të ndara në vitin e kaluar (t), dhe vitin e ardhshëm (t + 1).
δIt+1 / δIt ≡ I
Nga ana tjetër, kemi shkallën e zhvillimit teknologjik (T²). Këtu ne duhet të fillojmë me ndërtimin e produkteve finale teknologjike (output), “δV”, e cila është e bazuar në shumën totale të tre shumave të pafundësshme, nga përdorimi i shumave totale të patentave të regjistruara (∫Σαi), plus shumën totale të shitjeve të teknologjisë (∫Σβj) plus shuma totale e të gjitha projekteve që kanë të bëjnë me kërkimin, hulumtimin dhe zhvillimin (∫Σθk). Kështu, variabli “t” përfaqëson kohën, në modelin tonë, ne llogarisim kohën bazuar në normën e rritjes në mes të dy viteve. Për të matur shpejtësinë e zhvillimit teknologjik (T²), ne propozojmë për të aplikuar formulën origjinale për llogaritjen e shpejtësisë ku shpejtësia është, rruga, me kalimin e kohës (D/t); por në rastin tonë, distancën do ta zëvëndesojmë me produktin finalë teknologjikë (output), “ δV “.Ne supozojmë se shkalla e zhvillimit teknologjik (T²) nuk është një variabël konstant në ekuacionin tonë, e tillë si shpejtësia e dritës e shpjeguar në formulën E = MC². Ne sugjerojmë që para se të bëjmë matjen e produktit (output) Y, ta mbajmë variablën e zhvillimit teknologjik (T²) për shkak se sfidat e vazhdueshme të kërkimit, zhvillimit dhe inovacionit (RDI) ende mund të gjenerojnë një transformim të vazhdueshëm në prodhimin e mallrave dhe shërbimeve të reja në treg. Një tjetër arsye që T² duhet të jetë variabel është se fenomenet natyrore mund të maten me saktësi mbi bazën e eksperimentimit, të tilla si shpejtësia e dritës (C²). Në rastin e fenomeneve sociale si makroekonomia, ajo nuk mund të matet me një saktësi që bazohet në eksperiment në të njëjtin nivel siç është rasti me zhvillimet teknologjikë. Megjithatë, një tjetër arsye qe shpejtësia e zhvillimit teknologjik (T²) është eksponencialë në katror, është se supozojmë se shpejtësia e zhvillimit teknologjik mund të gjenerojnë efekt të dyfishtë mbi shumën përfundimtare të Y, në afat të shkurtër dhe të gjatë. Në këtë pjesë të modelit, do të aplikojmë diferencialet e pjesshme në matjen e δV i δT.
Së fundi, formula për Y është:
Y = IT2
Formula e mësiperme e prodhimit (output) (Y) mund të tregonë skenarë të shumtë, të tillë si:
-
Scenario- e parë në qoftë se ne kemi një normë të ulët të informacionit (I), për shembull nivelin e ulët të G2C, shumëzuar me shpejtësinë e zhvillimit teknologjik (T²) në katror, atëherë IT² së bashku mund të konvertohet në një sasi shumë të vogël të Y.
-
Scenario- i dytë në qoftë se ne kemi një shkallë të lartë të informacionit (I) shumëzuar me shpejtësinë e lartë të zhvillimit teknologjik në katror(T²), atëherë IT² së bashku mund të konvertohet në një sasi shumë të madhe të Y.
- Scenario- i treti në qoftë se ne kemi një normë të ulët të informacionit (I) shumëzuar me shpejtësinë e zhvillimit teknologjik të ulët në katror (T²), atëherë IT² së bashku mund të konvertohet në një sasi shumë të vogël të Y.
Tema u mbrojtë para komisionit të përbërë nga Prof. dr Maja Baqoviq – mentor (prorektor i Univerzitetit të Malit të Zi), Prof. dr Bilana Rondoviq, dhe docent dr Sasha Vujosheviq me notë mesatare 10.00 dhe njikosisht e propozuar për doktoraturë.